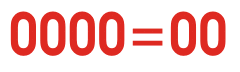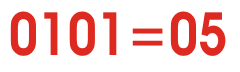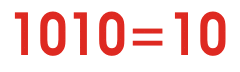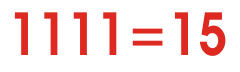二进制数制是什么?
在数字电子技术yabo和365哪个平台更大二进制数是提供数字输入最重要的工具。现在在理解之前二进制数字系统,我们必须了解我们在日常生活中使用的十进制数系。数字系统首先在人类历史中引入计数目的。
不同的计数用不同的符号表示。如一个单一的事物被一个符号1计数,如果有两个事物,该符号将为2,如果有三个事物计数,该符号为3。对于4、5、6、7、8、9,十进制中使用的符号分别是4、5、6、7、8和9。符号0(0)表示没有什么可以计数。所以0 1 2 3 4 5 6 7 8 9是10个基本符号用来从0数到9。这就是为什么它被称为十进制或以10为基数的十进制。
但是如果有超过九件事要计算,那么我们就不会去另一个新符号,而是我们将两个或更多符号从0到9组合,并表示超过九个的数字。对于代表九个+十分之一,我们使用10,我们使用的九个+两个我们使用11等。通过这种方式,我们建立了十进制数系。
现在来看看二进制数字系统——之所以这样命名是因为它有两个基数(0和1),它们用来表示整个数字系统。看下面的动画来了解二进制转换为十进制数。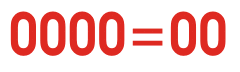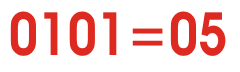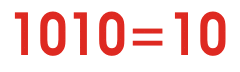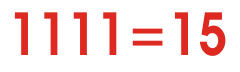
二元数系的历史
B.进制是在公元前5 -2世纪由印度学者平加拉引进的。他用长音节和短音节来说明这两种类型的数字,它更像莫尔斯电码。
1679年,戈特弗里德·莱布尼茨发明了现代二进制数字系统,至今仍在使用。
任何类型的数字(十进制)都可以由二进制数字系统表示。使用该系统在数字电子产品中流行,因为可以很容易地理解开启和关闭模式。yabo和365哪个平台更大
| 00 | 01. | 02. | 03. | 04. | 05. | 06. | 07. | 08. | 09. |
|---|---|---|---|---|---|---|---|---|---|
| 10. | 11. | 12. | 13. | 14. | 15. | 16. | 17. | 18. | 19. |
| 20. | 21. | 22. | 23. | 24. | 25. | 26. | 27. | 28. | 29. |
| 30. | 31. | 32. | 33. | 34. | 35. | 36. | 37. | 38. | 39. |
| 40 | 41. | 42. | 43. | 44. | 45. | 46. | 47. | 48. | 49. |
| 50. | 51. | 52. | 53. | 54. | 55. | 56. | 57. | 58. | 59. |
| 60. | 61. | 62. | 63. | 64. | 65. | 66. | 67. | 68. | 69. |
| 70 | 71. | 72. | 73. | 74. | 75. | 76. | 77. | 78. | 79. |
| 80 | 81. | 82. | 83. | 84. | 85. | 86. | 87. | 88. | 89. |
| 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 |
这里,在上表中,每个数字由任何两个基本符号(0到9)的组合表示。这些基本符号称为数字和这些数字的相应位置以表示的数量称为位。因此,上面表示的所有十进制数是两位数,双位数。数字中最左侧的位数被称为大多数有效位(MSB),其中大多数位是最低有效位(LSB)。
如果我们观察到上面给出的数字,我们会发现前十个连续数字,即00到09是通过在LSB的十进十进制数字中来表示。然后,MSB将更改为下一个连续的数字,并且通过更改LSB的数字在其他十个连续数字(从10到19)表示。在表中的第三行MSB将更改为下一个连续的数字,并且通过表示其他十个连续数字(从20到29)更改的数字。
一共有100个数字,即从00到99个数字用两位十进制表示。100意味着102这意味着(基本数字的数量)的比特数。因此是3位103.或1000年数字(我。e从000到999)可以表示。类似地,n位10N数字可以表示。
现在考虑一个数字系统只有两位数0和1.这个系统也可以在与十进制系统相同的逻辑中表示。只有两个数字0和1的数字系统称为二进制数系。
这里,归零由符号'0'表示,一个表示为'1',但如果数字大于一个,则MSB被改变为1,并且通过改变其他两个连续数字,可以表示。就像十进制系统一样,二进制系统计算的总数取决于它位。
对于二比特二进制,是22数字,即0到3可以表示。公式相同,用二进制数制表示的总数=(基本位数)的比特数。二进制系统的基本数字是2(0和1),但是位数可以从1到无穷任意选择,因此所有的数字范围都可以很容易地用二进制系统表示,就像所有其他的数字系统一样。
二进制数系定义
二进制数制被定义为以2为基数的数制。这意味着这个系统中的数字由两个数字组成- 1和0。
现在,考虑诸如625的十进制数。从非常基本的概念我们可以理解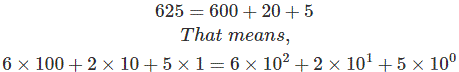
这里,625是三位十进制数,其LSB的最正确的数字或数字为5,如果我们从右计算比特,大多数位将是0.下一位从右边编号为1,这里有1个,下面的数字2同样,左边最多位为2,数字是6.所以从这个例子中很清楚任何十进制数可以表示为:
Σdigit×10对应位置或位
这里在上面的表达式10中是十进制系统中使用的数字的总数.. 0到9
与十进制系统一样,任何数字系统都可以由相同的表达式表示,表达式中只有10只能通过该系统中使用的总数字替换。因此,任何系统中的任何数字都可以表示为:
ΣDIGIT×(该系统中使用的数字数)对应位置或位
二进制数系中使用的数字数为2.因此,可以在本系统中表示任何数字:
∑数字×(2)对应位置或位
| 5. | 4. | 3. | 2 | 1 | 0. | →位置或一些 |
| 1 | 0. | 1 | 0. | 1 | 0. | →二进制数字 |
在这里,这是二进制数因此,101010.因此,根据上面的表达式,该数量可以表示为: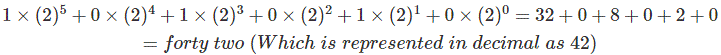
为了更好地理解,请遵守下表:
| 二进制数 | 十进制等价物 | ||||||||
| 位置 或者 |
7. | 6. | 5. | 4. | 3. | 2 | 1 | 0. | |
| 二进制 数字 |
0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0×27.+ 0×26.+ 0×25.+ 0×24.+ 0×23.+ 0×22+ 0×21+ 0×20.= 0. |
|---|---|---|---|---|---|---|---|---|---|
| 0. | 0. | 0. | 0. | 0. | 0. | 0. | 1 | 0×27.+ 0×26.+ 0×25.+ 0×24.+ 0×23.+ 0×22+ 0×21+1×20.= 1 | |
| 0. | 0. | 0. | 0. | 0. | 0. | 1 | 0. | 0×27.+ 0×26.+ 0×25.+ 0×24.+ 0×23.+ 0×22+1×21+ 0×20.= 2 | |
| 0. | 0. | 0. | 0. | 0. | 0. | 1 | 1 | 0×27.+ 0×26.+ 0×25.+ 0×24.+ 0×23.+ 0×22+1×21+1×20.= 3 | |
| 0. | 0. | 0. | 0. | 0. | 1 | 0. | 0. | 0×27.+ 0×26.+ 0×25.+ 0×24.+ 0×23.+1×22+ 0×21+ 0×20.= 4 | |
| 0. | 0. | 0. | 0. | 0. | 1 | 0. | 1 | 0×27.+ 0×26.+ 0×25.+ 0×24.+ 0×23.+1×22+ 0×21+1×20.= 5 | |
| 0. | 0. | 0. | 0. | 0. | 1 | 1 | 0. | 0×27.+ 0×26.+ 0×25.+ 0×24.+ 0×23.+1×22+1×21+ 0×20.= 6 | |
| 0. | 0. | 0. | 0. | 0. | 1 | 1 | 1 | 0×27.+ 0×26.+ 0×25.+ 0×24.+ 0×23.+1×22+1×21+1×20.= 7 | |
| 0. | 0. | 0. | 0. | 1 | 0. | 0. | 0. | 0×27.+ 0×26.+ 0×25.+ 0×24.+1×23.+ 0×22+ 0×21+ 0×20.= 8 | |
看到动画打击,了解如何计算不同的二进制数