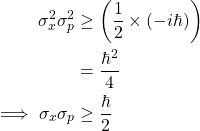内容

什么是heisenberg不确定性原则
这海森伯格不确定性原则是量子力学统计性质的更有趣和相应的结果之一。最着名的不确定性原则的实现指出,不能绝对确定量子系统的位置和势头来衡量。这是最常见的实现,发现全部受欢迎的科学。然而,不确定性原则比这更广泛。完全不确定性原则也具有不平等的特征。广义不确定性原则表示为:

只有这种广义关系的特殊情况适用于吸引最受关注的位置和动量。在本文中,我们将探讨衡量某些东西,不确定性原则,最后,海森伯格的不确定性原则(他们不一样!)。
这海森伯格不确定性原则是量子力学统计性质的结果。为了理解它,我们必须首先理解测量。
是什么
测量 在量子物理学中?
测量的行为使量子系统扰乱。例如,如果您要在文章中执行任何测量xinyabo购彩您会打扰粒子的底层电气系统(您也很快发现您无法衡量绝对确定性 - 但要在以后介绍)。
量子系统的干扰是因为过程测量实际上和作用于量子系统的波函数是一样的(这满足Schrodinger方程式)与操作员。
一旦算子作用于波函数,波函数将坍缩成与该算子对应的本征态。一口!让我们从这些术语中退一步回到最基本的原则。
我们来做一个关于光电效应通过试图测量狭缝另一端的粒子,粒子将降落(想象一下,你有一个统治者,你试图衡量沿着的地方轴粒子将降落)。早期量子物理学的主要结果之一是粒子表现得像波浪.
这意味着存在在沿着的任何地方找到粒子的非零概率轴。让我们看一下围绕位置测量的概率分布。如果我们有一个半某些想法,粒子所在的位置,误差(或标准偏差
)位置测量的分布看起来像:

如果我们以某种方式确切地知道粒子沿位置轴线的位置,概率分布看起来有点像:

如果我们几乎没有想到粒子位于狭缝的另一端的粒子,概率分布看起来像:

这是量子力学统计性质的地方。定性地,波函数为每个观察到的概率分布提供我们想要测量的(思考能量,动量,位置,总能量等)。
推导海森堡测不准原理
广义不确定性公式的推导将在后期介绍。第一理论里程碑与理解有关,每次要进行测量时,操作员都可以在代表量子系统的状态矢量上作用。对于位置,操作员(帽子意味着它是运营商):

所以当你测量一个量子系统的位置时,你要用状态乘以.对于动量,操作员看起来像:

这是围绕不兼容的可观察到的谈话来玩的地方。任何时候与观察到的操作员都有一个非零换向器,您就无法确定性地观察。两个运营商的换向器定义如下:

由广义测不准原理公式证实了我们所要测量的两个算子的换流子。现在让我们计算位置和动量的交换子:

因此,如果将此结果替换为广义不确定性原则公式,您可以获得着名的海森伯格不确定性原则:
这是着名的不确定性原则的实现。它可以解释如下:当您变得越来越肯定您的量子系统的位置(即,你就越不确定系统的动量(即动量)。
反之亦然。
同样,这是由于标准偏差将炸毁势头,因为标准偏差变小(更确定性)来维护不确定性原则。
引用
- Shankar r(1980)。量子力学原理.纽约:施普林格Science,第1版,第1-40页。
- Gasiorowicz,美国(2019年)。量子物理学.第二次。加拿大:汉密尔顿印花,第1-50页。