发病矩阵是表示图形的矩阵,使得借助该矩阵我们可以绘制图形。该矩阵可以表示为[aC[每个矩阵中,还有行和列发病矩阵[一种C]。
矩阵的行[aC]表示矩阵的节点数量和列[aC]表示给定图中的分支数。如果在给定的入射矩阵中存在“n”行,则在图中的含义中的指示有“n”节点。类似地,如果给定发射矩阵中存在“M”列,则该图形在该图中有“M”分支。
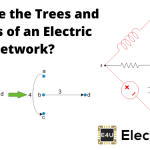
在上面显示的图形或指导图中,有4个节点和6个分支。就这样发病矩阵对于上图,图表将有4行和6列。
入射矩阵的条目始终为-1,0,+1。该矩阵始终类似于KCL.(Krichoff Current Law)。因此,从KCL我们可以得出那个,
| 分支的类型 | 价值 |
| 从k开始的分支TH.节点 | +1 |
| 进入k的分支TH.节点 | -1 |
| 其他 | 0. |
构建发病矩阵的步骤
以下是绘制发病率的步骤: -
- 如果是给定的kTH.节点具有外向分支,然后我们将写入+1。
- 如果是给定的kTH.节点有传入分支,然后我们将写入-1。
- 休息其他分支将被认为是0。
发病率的例子
对于上面所示的图表写入其入射矩阵。
降低发病率矩阵
如果来自给定的话发病矩阵[一种C[删除任何任意行,然后形成的新矩阵将减少入射矩阵。它由符号[a]表示。发病率降低的顺序是(n-1)×b,其中n是节点的数量,b是分支的数量。
对于上述图表,减少的发病率矩阵将是: -
[注意: - 在上面所示,删除矩阵4。]
现在让我们考虑与缩小发病矩阵相关的新示例。对于上面所示的图表写入其降低的入射矩阵。
回答:-为了排出较低的发病率,首先绘制其入射矩阵。它的发病矩阵是: -
现在绘制其发病率降低。为此,我们只需删除任何节点(在此中我们已删除节点2)。其发病率降低为: -
这是所需的答案。
要点要记住
- 用于检查我们绘制的发病矩阵的正确性,我们应该检查列的总和。
- 如果列的总和为零,那么我们创建的发生率矩阵是纠正的错误。
- 发射矩阵仅可以仅应用于指向图。
- 除零之外的行中的条目数告诉我们与该节点链接的分支的数量。这也称为该节点的程度。
- 完整的等级发病矩阵是(n-1),其中n是图形的节点的数量。
- 发射矩阵的顺序是(n×b),其中b是图表的分支的数量。
- 从给定的减少发病矩阵我们可以绘制完整的发病矩阵只需在每个列的总和应为零的条件下简单地添加+1,0或-1。